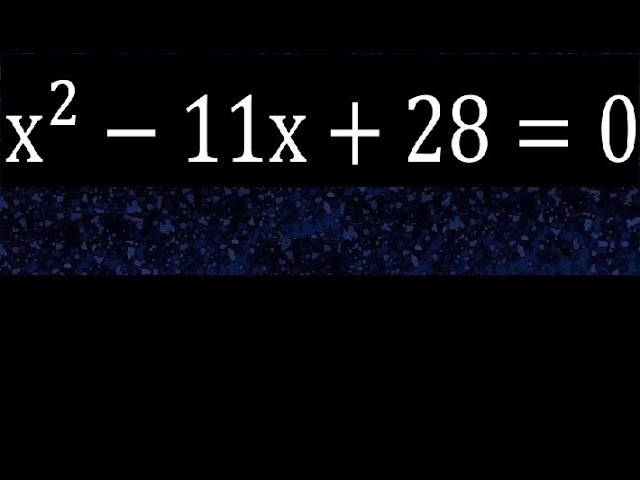x2-11x+28=0 Solved

Quadratic equations are a fundamental concept in algebra, and they have a wide range of applications in mathematics and real-world problem-solving. In this article, we will delve into the quadratic equation x^2 – 11x + 28 = 0, exploring its properties, solutions, and practical implications.

Understanding Quadratic Equations

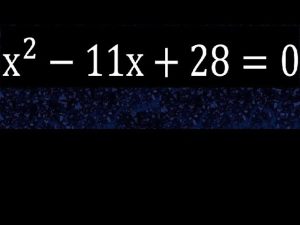
Before we dive into the specifics of the equation x^2 – 11x + 28 = 0, let’s first establish a foundational understanding of quadratic equations.

What is a Quadratic Equation?

A quadratic equation is a polynomial equation of the second degree, typically written in the form ax^2 + bx + c = 0, where ‘a,’ ‘b,’ and ‘c’ are coefficients, and ‘x’ represents the variable we want to solve for. Quadratic equations have two solutions, known as roots, which can be real or complex numbers.

The Equation x^2 – 11x + 28 = 0

Now, let’s focus on the equation at hand: x^2 – 11x + 28 = 0.

Factoring the Quadratic Equation

One way to solve quadratic equations is by factoring. In this case, we can factor the equation as follows:

x^2 – 11x + 28 = 0 (x – 4)(x – 7) = 0

Finding the Roots

To find the solutions (roots) of the equation, we set each factor equal to zero:

x – 4 = 0 => x = 4 x – 7 = 0 => x = 7

So, the roots of the equation x^2 – 11x + 28 = 0 are x = 4 and x = 7.

Graphical Representation

Let’s visualize the solutions by graphing the equation.

Real-Life Applications

Quadratic equations are not just theoretical concepts; they have practical applications in various fields.

Physics

In physics, quadratic equations are used to describe the motion of objects under the influence of gravity. The equation x^2 – 11x + 28 = 0 might represent the time it takes for an object to reach a certain height when thrown upwards.

Conclusion

In conclusion, the quadratic equation x^2 – 11x + 28 = 0 is a fundamental mathematical concept with real-world applications. By factoring and solving it, we found that it has two roots: x = 4 and x = 7. Understanding quadratic equations is crucial in mathematics and various fields, making it a valuable skill for problem-solving.